Indian Century

INDIAN MATHEMATICS AND PROMINENT MATHEMATICIANS

“The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged from India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and places arithmetic foremost amongst useful inventions.The importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius." Pierre-Simon Laplace.

"We owe a lot to the Indians, who taught us how to count, without which no worthwhile scientific discovery could have been made". Albert Einstein.

"From the earliest numerate civilisation of the Indus valley, through the scholars of the 5th to 12th centuries who were conversant in arithmetic, algebra, trigonometry, geometry combinatorics and latterly differential calculus, Indian scholars led the world in the field of mathematics. The peak coming between the 14th and 16th centuries in the far South, where scholars were the first to derive infinite series expansions of trigonometric functions." So wrote Ian G Pearce of University of St. Andrews in Scotland, in his masterly treatise on Indian Mathematics. He continues: " In addition to mighty contributions to all the principal areas of mathematics, Indian scholars were responsible for the creation, and refinement of the current decimal place value system of numeration, including the number zero, without which higher mathematics would not be possible. The purpose of my project is to highlight the major mathematical contributions of Indian scholars and further to emphasise where neglect has occurred and hence elucidate why the Eurocentric ideal is an injustice and, in some cases, complete fabrication." Please click on the link below or copy and paste the URL to the search bar to access the treatise.

https://mathshistory.st-andrews.ac.uk/Projects/Pearce/chapter-1/

Also please click on the following link to an equally masterful YouTube presentation, entitled: “the History of Hindu Numerals” and the next link, the same author(s) are dealing with Kerala and Madhava School of astronomy and mathematics and proof of how they invented Calculus, at least 300 years before the Europeans.

The history of Hindu numerals: when, where, who and how, they were invented

https://youtube/pYiRq0rHvKE

In the long and distinguished history of India, it has scored many firsts. It made the first civilization (at least three thousand years before the Sumerians), it was the first country to experiment with democracy (in a town called Vaishali in present day state of Bihar), centuries before the Greeks, the first to codify medical and surgical practice (Charaka and Susruta respectively), the first to organize religion(Hinduism) and delve deep into theology and philosophy, develop the systems of Yoga and Meditation (now all the rage in the world), create the first written language (Tamil), and the mother of all Indo-European languages (Sanskrit) and to delve into writing great treatises in both verse and prose, the first to recognize gravitation (this was at least a Millennium before Newton), the first to describe the elliptical orbits of planets around the sun, to describe how solar and lunar eclipses occur, theorize that earth rotated on its axis, thus giving the illusion of heavenly bodies revolving around earth, (all of these predated the Europeans by more than a millennium!), the first to produce steel, invent the game of chess, invent martial arts (“KalarippayatT”) etc, etc. However, India’s greatest gift to the world was in the field of mathematics. India pioneered almost every field of mathematics, from the Hindu or Indian numeral system (1-9, previously and erroneously called the "Arabic numerals") the invention of zero and the decimal place value system, the arithmetical principles of addition, subtraction, multiplication and division, the notion of infinity, geometry and many of the theorems traditionally attributed and named after the Greeks or other Europeans, algebra, trigonometry and even significant parts of calculus were all developed by Indians to a significant degree of finesse, all long before any country or individual that the Europeans have given such credits to.

In presenting India’s gift of mathematics to the world, I will adopt the following format:

1) How and why mathematics originated in India.

2) The evolution of mathematics in early India, including the Indian numeral and place value systems, and the invention of zero.

3) Prominent practitioners of mathematics through India’s history and their contributions to the field.As there are numerous mathematicians of renown in India’s history, only the most important and pivotal personalities will be discussed in separate sections. In some instances, and when appropriate, the work of some of the mathematicians may be covered within the text of discussion topic.

When appropriate, a more focused description of systems or schools of mathematics in different parts of India.

1) HOW AND WHY MATHEMATICS ORIGINATED IN INDIA:

Everyone recognizes that the earliest contribution of India to this field was the ten-base system, but actual dates are not known. In order to keep this section factual, I will restrict my descriptions to mostly what is historically known. However, as new information becomes available, this section will necessarily need revision. We now know that at least a large city-dwelling population existed in a place called Dwarka (which is now submerged off the coast of Gujarat. (Please check this video presentation: www.indiancentury.com/dwar.htm), approximately 9,500 years ago. If recordings from this city show mathematical notations, clearly the story of mathematics will become that much older.

What is historically known goes back to the days of the Harappa civilization, 2600-3000 BCE. Since this Indian civilization delved into commerce and cultural activities, it was only natural that they devise systems of weights and measurements. For example, a bronze rod marked in units of 0.367 inches was discovered and point to the degree of accuracy they demanded. Evidently, such accuracy was required for town planning and construction projects. Weights corresponding to 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200 and 500 have been discovered and they obviously played important parts in trade and commerce development.

The next phases of mathematics developments are found in Vedic texts, along with ritual practices, and in the Puranas. Calculations for the precise building of ritual altars would have been important, for obvious reasons. Arithmetic principles such as addition, subtraction, multiplication, fractions, cubes, squares and roots were developed during these periods (Narad Vishnu Purana (by Ved Vyas ~1000 BCE)). Geometric principles (“Rekha-ganit) are found in the Sulva Sutras, authored by Baudhayana (800 BCE) and Apasthamba (600 BCE). Calculations of one geometric shape (for example a rectangle) and converting them to an equivalent (or fraction or multiple thereof) square or circle would require a good working knowledge of geometry. Pythagoras, who studied mathematics in India (6^th century BCE), became familiar with the principles of geometry from the Sulva Sutras .Even the so-called Pythagoras theorem was described by Baudhayana in his Sutra. (“The chord that is stretched across the diagonal of a square produces an area of double the size”). His Sutra also contained geometric solutions of a linear equation in a single unknown and even examples of quadratic equations. Apasthamba Sutra described calculation of the value for the square root of 2, accurate to the fifth decimal place. A solution to the general linear equation is also described in this Sutra and the squaring of a circle and dividing a segment into seven equal parts.

THE EVOLUTION OF MATHEMATICS IN INDIA:

INDIAN NUMERAL SYSTEM:

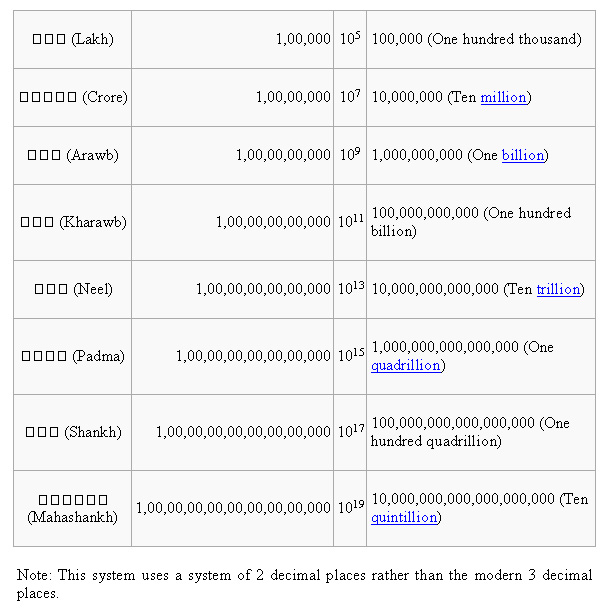
The Indian number system is exclusively a base 10 system, in contrast to the Babylonian system, which was base 60; for example, the calculation of time in seconds, minutes and hours. The three tables given above depict representation of Indian numerals at different times, and they partly portray the evolution of the numerals. The development and common use of this numeral system in India was recorded by the Arabic scholar and mathematician al-Biruni in approx. 1020 AD. He made several trips to India, studying the Indian Philosophy and Mathematics and he wrote 27 works on India. Regarding the numerals he wrote:

“Whilst we use letters for calculation according to their numerical value, the Indians do not use letters at all for arithmetic. And just as shape of the letters that they use for writing is different in different regions of their country, so the numerical symbols vary”. “What we (the Arabs) use for numerals is a selection of the best and most regular figures in India”.

Another special aspect of the Indian numeral system is the place-value system that is embedded in it. This means that each numeral is given a value related to its position in the count, relative to the other numerals. In itself, this is not unique to the Indian numeral system and Indians were not the earliest to make such assignments. Babylonians also ascribed relative values to each numeral but their system’s flaw was that it was a base 60 system. The origin of the modern decimal-based place value system is ascribed to Aryabhata I, 498 CE. Or at least he was aware of this system as noted below: This fact is clear in his statement: “Sthanam sthanam dasa gunam” (“place to place in ten times in value”). The oldest record of this value place assignment is in a document recorded in 594 CE, a donation charter of Dadda III of Sankheda in Bharukachcha region. No satisfactory explanation exists as to why the Greeks did not develop this place value system; one can only conjecture that this was due to the inherent deficiency of the base 60 system that they adopted from the Babylonians .The Chinese system employed pseudo-positional number rods, which some claim was transmitted to the Indians and became the basis of the Indian numeral system. Some have also claimed that the Indians derived their numeral system from Archimedes’ Sand-reckoner. What is undisputed, however, is that the Indian numeral system is the basis of the modern numerals everywhere and that it was transmitted to the rest of the world by the Arabs.

In support of the Indians' contribution to developing the place value system is an entry by the French mathematician Georges Ifrah, who wrote in his book "Universal History of Numbers":

" Thus it would seem highly probable under the circumstances that the discovery of zero and the place-value system were inventions unique to the Indian civilization. As the Brahmi notation of the first nine whole numbers (incontestably the graphical origin of our present-day numerals and of all the decimal numeral systems in use in India, Southeast and Central Asia and the Near East) was autochthonous and free of any outside influence, there can be no doubt that our decimal place-value system was born in India and was the product of Indian civilization alone."

Another illuminating record of the use of the Indian Numerals, the place value system and of zero came from the Italian mathematician Fibonacci. He stated thus:

“After my father’s appointment by his homeland as state official in the customs house of Bugia for the Pisan merchants who thronged to it, he took charge; and in view of its future usefulness and convenience, had me in my boyhood come to him and there wanted me to devote myself to and be instructed in the study of calculation for some days. There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily and Provence, with their varying methods; and at these places thereafter, while on business. I pursued my study in depth and learned the give-and-take of disputation. But all this even, and the algorism, as well as the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus (Modus Indorum).Therefore, embracing more stringently that method of the Hindus, and taking stricter pains in its study, while adding certain things from my own understanding and inserting also certain things from the niceties of Euclid’s geometric art. I have strived to compose this book in its entirety as understandably as I could, dividing it into fifteen chapters. Almost everything which I have introduced I have displayed with exact proof, in order that those further seeking this knowledge, with its pre-eminent method, might be instructed, and further, in order that the Latin people might not be discovered to be without it, as they have been up to now. If I have perchance omitted anything more or less proper or necessary, I beg indulgence, since there is no one who is blameless and utterly provident in all things. The Indian figures are: 9 8 7 6 5 4 3 2 1.With these nine figures and with the sign 0… any number may be written.”

GREEK AND ROMAN NUMERALS:

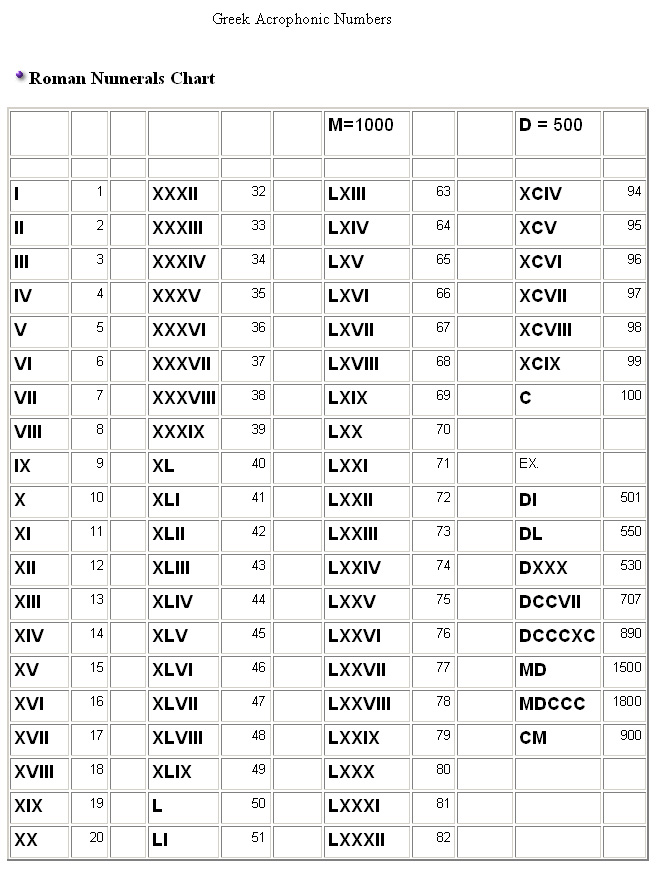
The earliest recorded inscription of decimal digits to include the symbol for the digit zero, a small circle, was found at the Chaturbhuja Temple at Gwalior, India, dated 876 CE. The oldest known text to use a decimal place-value system, including zero was found in a Jain text from India, the Lokavibhaga, and dated 458 CE. Thus, assigning a different character for each digit as well as the place value system and the addition of a zero to form the decimal system enabled Indians to write numbers of any value. Babylonians used a space between their sexagesimal numerals for a positional value; however, they did not use zero as a separate number. By 300 BCE two slanted wedges were used as a punctuation symbol for a place-holder in the Babylonian system. Again, they did not use this ‘zero’ as a separate number. The Mesoamerican Long Count calendar from South Central Mexico and Central America did use a zero as a place-holder in their vigesimal (base 20) positional numeral system. This invention is credited to the Olmecs, around the end of the 4^th century BCE. Zero was not, however, used by the Olmecs as a separate number. The Chinese used counting rods for calculations as early as the 4^th century BCE. They understood the negative numbers and zero but they had no symbol for zero until the age of the Song Dynasty in 1247 when the mathematician Qin Jiushao proposed a symbol for zero.

The rules for the use of zero were written down first by Brahmagupta, in his book “Brahmasputha Siddhanta” (The Opening of the Universe) in the year 628 CE.He also considered negative numbers in his teachings. The following are the rules of Brahmagupta:

1) The sum of zero and a negative number is negative.

2) The sum of zero and a positive number is positive.

3) The sum of zero and zero is zero.

4) The sum of a positive and a negative is their difference; or, if their absolute values are equal, zero.

5) A positive or negative number when divided by zero is a fraction, with zero as denominator.

6) Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator.

7) Zero divided by zero is zero. The modern systems do not assign a number

to this equation.

I will end this section with the following quotation from G.B. Halsted:

“The importance of the creation of the zero mark can never be exaggerated. This giving to airy nothing, not merely a local habitation and a name, a picture, a symbol, but helpful power, is the characteristic of the Hindu race from whence it sprang. It is like coining the Nirvana into dynamos. No single mathematical creation has been more potent for the general on-go of intelligence and power.”

JAINA MATHEMATICS

Jaina mathematicians were practitioners of Jainism and belong to the period following 6^th century have the distinction of being a bridge between the Vedic Period in mathematics to the so-called Classical Period. They are also credited with extricating mathematics from religious rituals, as used to be the case with the Hindus. Jains’ fascination with large numbers directly led them to classifying such large numbers into the enumerable, the innumerable or the infinite. Jain mathematicians are credited with defining infinity into many types: infinity in one direction, infinity in two directions, the infinite in area, the infinite everywhere and the infinite perpetually. A well-recognized Jaina mathematician is Pingala (300 ~ 200 BCE).Although not strictly a mathematician but a musical theorist, he is credited with stumbling upon the Binary numeral system. He is also credited with discovering the “Pascal triangle” and the Binominal coefficient. Basic concepts of the Fibonacci numbers have also been described by Pingala.

BAKSHALI MANUSCRIPT:

Written on birch bark, this is the oldest manuscript on mathematics in South Asia. This was accidentally discovered by a farmer while digging in a place called Bakshali near the modern city of Peshawar, now in Pakistan. The manuscript is now preserved in the Bodleian Library in Oxford University. No one is certain about the date of the manuscript, but it is widely considered to date between the 7^th and 12^th century CE. Topics in arithmetic, algebra and arithmetic progression are discussed in some detail in these manuscripts.

PROMINENTPRACTITIONERS OF MATHEMATICS

In order to cover the field in a consistent manner, I will present the most significant practitioners of Indian mathematics strictly in a chronological order. Also, for the sake of brevity, only the most important mathematicians and their contributions will be outlined.